轉載自http://www.cnblogs.com/jmp0xf/archive/2013/05/14/Bias-Variance_Decomposition.html
偏差bias計算公式?完全退化了,不會分解,看到別人的分解方法了,留存。
以下為轉載:
?
-----我是轉載的昏割線-----
?
設希望估計的真實函數為
?
?
但是觀察值會帶上噪聲,通常認為其均值為0
?
?
假如現在觀測到一組用來訓練的數據
?
?
那么通過訓練集估計出的函數為
?
?
為簡潔起見,以下均使用f^(X)代替f^(X;D)
?
那么訓練的目標是使損失函數的期望最小(期望能表明模型的泛化能力),通常損失函數使用均方誤差MSE(Mean Squred Error)
?
?
注意:?yi和f^都是不確定的;?f^依賴于訓練集D,?yi依賴于xi.
?
下面單獨來看求和式里的通項
E[(yi?f^(xi))2]=E[(yi?f(xi)+f(xi)?f^(xi))2]
=E[(yi?f(xi))2]+E[(f(xi)?f^(xi))2]+2E[(yi?f(xi))(f(xi)?f^(xi))]?
=E[?2]+E[(f(xi)?f^(xi))2]+2(E[yif(xi)]?E[f2(xi)]?E[yif^(xi)]+E[f(xi)f^(xi)])
=Var{noise}+E[(f(xi)?f^(xi))2]
E[yif(xi)]=f2(xi)??因為f和xi是確定的而E[yi]=f(xi)
E[f2(xi)]=f2(xi)??因為f和xi是確定的
E[yif^(xi)]=E[(f(xi)+?)f^(xi)]=E[f(xi)f^(xi)+?f^(xi)]=E[f(xi)f^(xi)]
E[?f^(xi)]=0??因為測試集中的噪聲?獨立于回歸函數的預測f^(xi)
E[?2]=Var{noise}??噪聲方差
?
E[(f(xi)?f^(xi))2]=E[(f(xi)?E[f^(xi)]+E[f^(xi)]?f^(xi))2]
=E[(f(xi)?E[f^(xi)])2]+E[(E[f^(xi)]?f^(xi))2]+2E[(f(xi)?E[f^(xi)])(E[f^(xi)]?f^(xi))]
=E[(f(xi)?E[f^(xi)])2]+E[(E[f^(xi)]?f^(xi))2]+2(E[f(xi)E[f^(xi)]]?E[E[f^(xi)]2]?E[f(xi)f^(xi)]+E[E[f^(xi)]f^(xi)])
=bias2{f^(xi)}+variance{f^(xi)}?
E[f(xi)E[f^(xi)]]=f(xi)E[f^(xi)]??因為f是確定的
E[E[f^(xi)]2]=E[f^(xi)]2
E[f(xi)f^(xi)]=f(xi)E[f^(xi)]??因為f是確定的
E[E[f^(xi)]f^(xi)]=E[f^(xi)]2
E[(f(xi)?E[f^(xi)])2]=bias2{f^(xi)}??偏差
E[(E[f^(xi)]?f^(xi))2]=variance{f^(xi)}??方差
?
最終
?
?
?
?
因此,要使損失函數的期望E[Loss(Y,f^)]最小,既可以降低bias,也可以減少variance。這也是為什么有偏的算法在一定條件下比無偏的算法更好。
?
偏差 bias 描述的是算法依靠自身能力進行預測的平均準確程度
方差 variance 則度量了算法在不同訓練集上表現出來的差異程度
?
下面來自The Elements of Statistical Learning?P38 Figure 2.11 的圖則闡釋了模型復雜度與偏差、方差、誤差之間的關系:
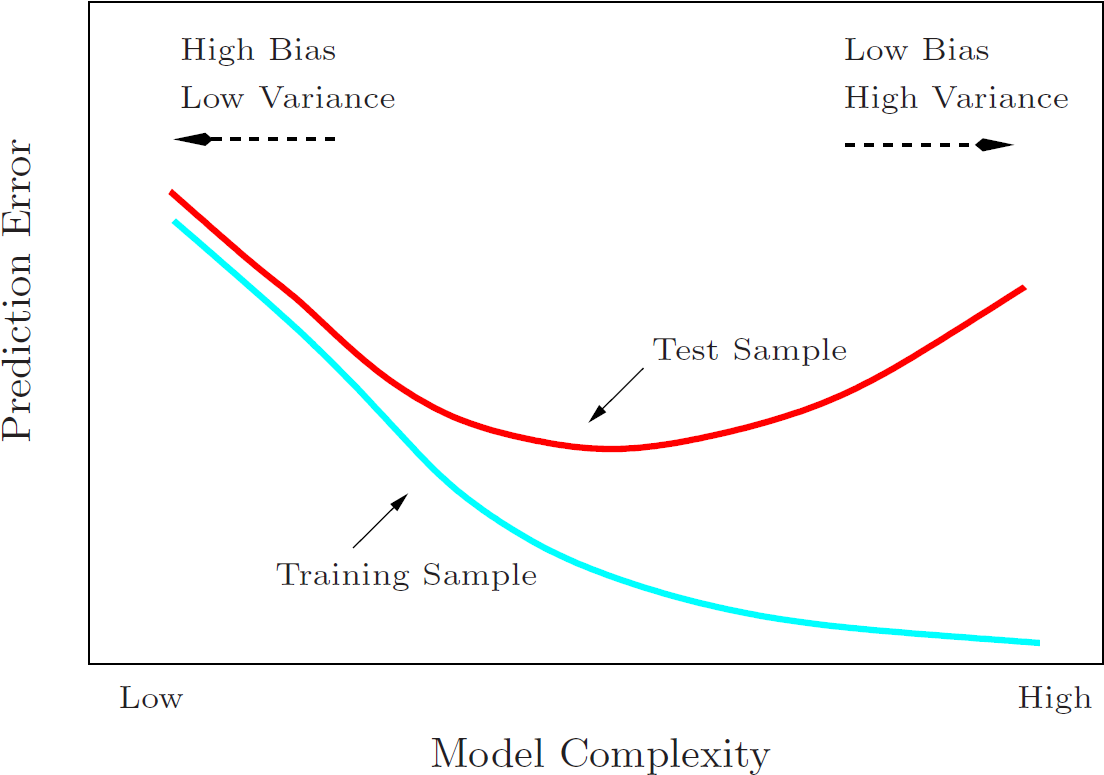
?
PS:
裝袋算法Bagging通過bootstrap對訓練集重采樣來并行訓練多個分類器(均勻采樣),主要是降低方差 variance。
提升算法Boosting通過迭代調整樣本權重來串行組合加權分類器(根據錯誤率采樣),因而主要是降低偏差 bias(同時也減少方差 variance)。
?
?
參考資料:
http://www.inf.ed.ac.uk/teaching/courses/dme/2012/slides/ensemble.pdf
http://www.inf.ed.ac.uk/teaching/courses/mlsc/Notes/Lecture4/BiasVariance.pdf
http://www.dna.caltech.edu/courses/cns187/references/geman_etal.pdf