? ? ? ? ? ?支持向量機原理(一) 線性支持向量機
支持向量機原理(二) 線性支持向量機的軟間隔最大化模型
支持向量機原理(三)線性不可分支持向量機與核函數
支持向量機原理(四)SMO算法原理
支持向量機原理(五)線性支持回歸
支持向量機算法的研究及其應用。?
在SVM的前三篇里,我們優化的目標函數最終都是一個關于$\alpha$向量的函數。而怎么極小化這個函數,求出對應的$\alpha$向量,進而求出分離超平面我們沒有講。本篇就對優化這個關于$\alpha$向量的函數的SMO算法做一個總結。
1. 回顧SVM優化目標函數
我們首先回顧下我們的優化目標函數:$$ \underbrace{ min }_{\alpha} ?\frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jK(x_i,x_j) - \sum\limits_{i=1}^{m}\alpha_i $$ $$ s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0 $$ $$0 \leq \alpha_i \leq C$$
我們的解要滿足的KKT條件的對偶互補條件為:$$\alpha_{i}^{*}(y_i(w^Tx_i + b) - 1 + \xi_i^{*}) = 0$$
根據這個KKT條件的對偶互補條件,我們有:$$\alpha_{i}^{*} = 0 \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b)?\geq?1 $$ $$ 0 <\alpha_{i}^{*}?< C ?\Rightarrow y_i(w^{*} \bullet \phi(x_i) + b)?=?1 $$ $$\alpha_{i}^{*}=?C \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b)?\leq 1$$
由于$w^{*} = \sum\limits_{j=1}^{m}\alpha_j^{*}y_j\phi(x_j)$,我們令$g(x) = w^{*} \bullet \phi(x) + b =\sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x, x_j)+ b^{*}$,則有: $$\alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i)?\geq?1 $$ $$ 0 < \alpha_{i}^{*}?< C ?\Rightarrow y_ig(x_i)??=?1 $$ $$\alpha_{i}^{*}=?C \Rightarrow y_ig(x_i)??\leq 1$$
2. SMO算法的基本思想
支持向量機算法應用。 上面這個優化式子比較復雜,里面有m個變量組成的向量$\alpha$需要在目標函數極小化的時候求出。直接優化時很難的。SMO算法則采用了一種啟發式的方法。它每次只優化兩個變量,將其他的變量都視為常數。由于$\sum\limits_{i=1}^{m}\alpha_iy_i = 0$.假如將$\alpha_3, \alpha_4, ..., \alpha_m$ 固定,那么$\alpha_1, \alpha_2$之間的關系也確定了。這樣SMO算法將一個復雜的優化算法轉化為一個比較簡單的兩變量優化問題。
為了后面表示方便,我們定義$K_{ij} = \phi(x_i) \bullet \phi(x_j)$
由于$\alpha_3, \alpha_4, ..., \alpha_m$都成了常量,所有的常量我們都從目標函數去除,這樣我們上一節的目標優化函數變成下式:$$\;\underbrace{ min }_{\alpha_1, \alpha_1} \frac{1}{2}K_{11}\alpha_1^2 + \frac{1}{2}K_{22}\alpha_2^2 +y_1y_2K_{12}\alpha_1 \alpha_2 -(\alpha_1 + \alpha_2)?+y_1\alpha_1\sum\limits_{i=3}^{m}y_i\alpha_iK_{i1} + y_2\alpha_2\sum\limits_{i=3}^{m}y_i\alpha_iK_{i2}$$ $$s.t. \;\;\alpha_1y_1 + ?\alpha_2y_2 = -\sum\limits_{i=3}^{m}y_i\alpha_i = \varsigma?$$ $$0 \leq \alpha_i \leq C \;\; i =1,2$$
3. SMO算法目標函數的優化
為了求解上面含有這兩個變量的目標優化問題,我們首先分析約束條件,所有的$\alpha_1, \alpha_2$都要滿足約束條件,然后在約束條件下求最小。
根據上面的約束條件$\alpha_1y_1 + ?\alpha_2y_2? = \varsigma\;\;0 \leq \alpha_i \leq C \;\; i =1,2$,又由于$y_1,y_2$均只能取值1或者-1, 這樣$\alpha_1, \alpha_2$在[0,C]和[0,C]形成的盒子里面,并且兩者的關系直線的斜率只能為1或者-1,也就是說$\alpha_1, \alpha_2$的關系直線平行于[0,C]和[0,C]形成的盒子的對角線,如下圖所示:
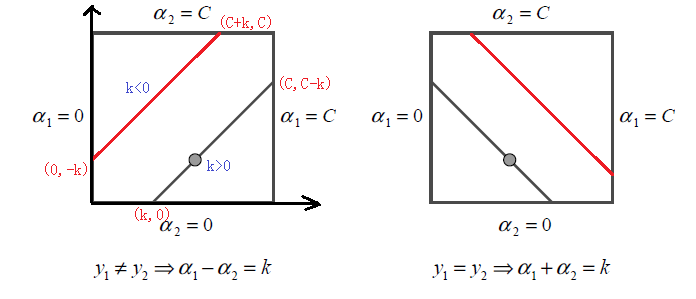
支持向量機算法,? 由于$\alpha_1, \alpha_2$的關系被限制在盒子里的一條線段上,所以兩變量的優化問題實際上僅僅是一個變量的優化問題。不妨我們假設最終是$\alpha_2$的優化問題。由于我們采用的是啟發式的迭代法,假設我們上一輪迭代得到的解是$\alpha_1^{old}, \alpha_2^{old}$,假設沿著約束方向$\alpha_2$未經剪輯的解是$\alpha_2^{new,unc}$.本輪迭代完成后的解為$\alpha_1^{new}, \alpha_2^{new}$
由于$\alpha_2^{new}$必須滿足上圖中的線段約束。假設L和H分別是上圖中$\alpha_2^{new}$所在的線段的邊界。那么很顯然我們有:$$L \leq \alpha_2^{new} \leq H $$
而對于L和H,我們也有限制條件如果是上面左圖中的情況,則$$L = max(0, \alpha_2^{old}-\alpha_1^{old}) \;\;\;H = min(C, C+\alpha_2^{old}-\alpha_1^{old})$$
如果是上面右圖中的情況,我們有:$$L = max(0, \alpha_2^{old}+\alpha_1^{old}-C) \;\;\; H = min(C, \alpha_2^{old}+\alpha_1^{old})$$
? 也就是說,假如我們通過求導得到的$\alpha_2^{new,unc}$,則最終的$\alpha_2^{new}$應該為:
$$\alpha_2^{new}=
\begin{cases}
H& { \alpha_2^{new,unc}?> H}\\
\alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc}?\leq H}\\
L& {\alpha_2^{new,unc} < L}
\end{cases}$$
神經網絡算法。 那么如何求出$\alpha_2^{new,unc}$呢?很簡單,我們只需要將目標函數對$\alpha_2$求偏導數即可。
首先我們整理下我們的目標函數。
為了簡化敘述,我們令$$E_i = g(x_i)-y_i = \sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x_i, x_j)+ b - y_i$$,
其中$g(x)$就是我們在第一節里面的提到的$$g(x) = w^{*} \bullet \phi(x) + b =\sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x, x_j)+ b^{*}$$
我們令$$v_i = \sum\limits_{j=3}^{m}y_j\alpha_jK(x_i,x_j) = g(x_i) - ?\sum\limits_{j=1}^{2}y_j\alpha_jK(x_i,x_j) -b ?$$
這樣我們的優化目標函數進一步簡化為:$$W(\alpha_1,\alpha_2) = \frac{1}{2}K_{11}\alpha_1^2 + \frac{1}{2}K_{22}\alpha_2^2 +y_1y_2K_{12}\alpha_1 \alpha_2 -(\alpha_1 + \alpha_2)?+y_1\alpha_1v_1 + ?y_2\alpha_2v_2$$
有限向量機, 由于$\alpha_1y_1 + ?\alpha_2y_2 = ?\varsigma?$,并且$y_i^2 = 1$,可以得到$\alpha_1用 \alpha_2$表達的式子為:$$\alpha_1 = y_1(\varsigma? - \alpha_2y_2)$$
將上式帶入我們的目標優化函數,就可以消除$\alpha_1$,得到僅僅包含$\alpha_2$的式子。$$W(\alpha_2) = \frac{1}{2}K_{11}(\varsigma? - \alpha_2y_2)^2 + \frac{1}{2}K_{22}\alpha_2^2 +y_2K_{12}(\varsigma?- \alpha_2y_2) \alpha_2 - (\varsigma? - \alpha_2y_2)y_1?-? \alpha_2 +(\varsigma? - \alpha_2y_2)v_1 + ?y_2\alpha_2v_2$$
忙了半天,我們終于可以開始求$\alpha_2^{new,unc}$了,現在我們開始通過求偏導數來得到$\alpha_2^{new,unc}$。
$$\frac{\partial W}{\partial \alpha_2} = K_{11}\alpha_2 + ?K_{22}\alpha_2 -2K_{12}\alpha_2 - ?K_{11}\varsigma?y_2 + K_{12}\varsigma?y_2 +y_1y_2 -1 -v_1y_2 +y_2v_2 = 0$$
整理上式有:$$(K_{11} +K_{22}-2K_{12})\alpha_2 = y_2(y_2-y_1 + \varsigma? K_{11} -?\varsigma? K_{12} + v_1 - v_2)$$
$$ =?y_2(y_2-y_1 + \varsigma? K_{11}?- \varsigma? K_{12} + (g(x_1) - ?\sum\limits_{j=1}^{2}y_j\alpha_jK_{1j} -b ) -(g(x_2) - ?\sum\limits_{j=1}^{2}y_j\alpha_jK_{2j} -b))$$
編碼向量。 將$?\varsigma? = \alpha_1y_1 + ?\alpha_2y_2 $帶入上式,我們有:
$$(K_{11} +K_{22}-2K_{12})\alpha_2^{new,unc} = y_2((K_{11} +K_{22}-2K_{12})\alpha_2^{old}y_2 +y_2-y_1 +g(x_1) - g(x_2))$$
$$\;\;\;\; = (K_{11} +K_{22}-2K_{12})?\alpha_2^{old} + y_2(E_1-E_2)$$
我們終于得到了$\alpha_2^{new,unc}$的表達式:$$\alpha_2^{new,unc} = \alpha_2^{old} + \frac{y_2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
利用上面講到的$\alpha_2^{new,unc}$和$\alpha_2^{new}$的關系式,我們就可以得到我們新的$\alpha_2^{new}$了。利用$\alpha_2^{new}$和$\alpha_1^{new}$的線性關系,我們也可以得到新的$\alpha_1^{new}$。
4. SMO算法兩個變量的選擇
SMO算法需要選擇合適的兩個變量做迭代,其余的變量做常量來進行優化,那么怎么選擇這兩個變量呢?
4.1 第一個變量的選擇
支持向量機的基本思想、 SMO算法稱選擇第一個變量為外層循環,這個變量需要選擇在訓練集中違反KKT條件最嚴重的樣本點。對于每個樣本點,要滿足的KKT條件我們在第一節已經講到了:?$$\alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i)?\geq?1 $$ $$ 0 < \alpha_{i}^{*}?< C ?\Rightarrow y_ig(x_i)??=1 $$ $$\alpha_{i}^{*}=?C \Rightarrow y_ig(x_i)??\leq 1$$
一般來說,我們首先選擇違反$0 < \alpha_{i}^{*}?< C ?\Rightarrow y_ig(x_i)??=1 $這個條件的點。如果這些支持向量都滿足KKT條件,再選擇違反$\alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i)?\geq?1 $?和 $\alpha_{i}^{*}=?C \Rightarrow y_ig(x_i)??\leq 1$的點。
4.2 第二個變量的選擇
? SMO算法稱選擇第二一個變量為內層循環,假設我們在外層循環已經找到了$\alpha_1$, 第二個變量$\alpha_2$的選擇標準是讓$|E1-E2|$有足夠大的變化。由于$\alpha_1$定了的時候,$E_1$也確定了,所以要想$|E1-E2|$最大,只需要在$E_1$為正時,選擇最小的$E_i$作為$E_2$, 在$E_1$為負時,選擇最大的$E_i$作為$E_2$,可以將所有的$E_i$保存下來加快迭代。
如果內存循環找到的點不能讓目標函數有足夠的下降, 可以采用遍歷支持向量點來做$\alpha_2$,直到目標函數有足夠的下降, 如果所有的支持向量做$\alpha_2$都不能讓目標函數有足夠的下降,可以跳出循環,重新選擇$\alpha_1$
4.3 計算閾值b和差值$E_i$
在每次完成兩個變量的優化之后,需要重新計算閾值b。當$0 < \alpha_{1}^{new}?< C$時,我們有 $$y_1 - \sum\limits_{i=1}^{m}\alpha_iy_iK_{i1} -b_1 = 0 $$
于是新的$b_1^{new}$為:$$b_1^{new} = y_1 - \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1}?- \alpha_{1}^{new}y_1K_{11} - \alpha_{2}^{new}y_2K_{21}?$$
簡述支持向量機的基本原理、 計算出$E_1$為:$$E_1 = g(x_1) - y_1 = \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1} + \alpha_{1}^{old}y_1K_{11} + \alpha_{2}^{old}y_2K_{21} + b^{old} -y_1$$
可以看到上兩式都有$y_1 - \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1}$,因此可以將$b_1^{new}$用$E_1$表示為:$$b_1^{new} = -E_1 -y_1K_{11}(\alpha_{1}^{new} - \alpha_{1}^{old}) -y_2K_{21}(\alpha_{2}^{new} - \alpha_{2}^{old}) + b^{old}$$
同樣的,如果$0 < \alpha_{2}^{new}?< C$, 那么有:$$b_2^{new} = -E_2 -y_1K_{12}(\alpha_{1}^{new} - \alpha_{1}^{old}) -y_2K_{22}(\alpha_{2}^{new} - \alpha_{2}^{old}) + b^{old}$$
最終的$b^{new}$為:$$b^{new} = \frac{b_1^{new} + b_2^{new}}{2}$$
得到了$b^{new}$我們需要更新$E_i$:$$E_i = \sum\limits_{S}y_j\alpha_jK(x_i,x_j) + b^{new} -y_i?$$
其中,S是所有支持向量$x_j$的集合。
最小二乘支持向量機原理? 好了,SMO算法基本講完了,我們來歸納下SMO算法。
5. SMO算法總結
輸入是m個樣本${(x_1,y_1), (x_2,y_2), ..., (x_m,y_m),}$,其中x為n維特征向量。y為二元輸出,值為1,或者-1.精度e。
輸出是近似解$\alpha$
1)取初值$\alpha^{0} = 0, k =0$
2)按照4.1節的方法選擇$\alpha_1^k$,接著按照4.2節的方法選擇$\alpha_2^k$,求出新的$\alpha_2^{new,unc}$。$$\alpha_2^{new,unc} = \alpha_2^{k} + \frac{y_2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
3)按照下式求出$\alpha_2^{k+1}$
支持向量機算法原理?$$\alpha_2^{k+1}=
\begin{cases}
H& {L \leq \alpha_2^{new,unc}?> H}\\
\alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc}?\leq H}\\
L& {\alpha_2^{new,unc} < L}
\end{cases}$$
4)利用$\alpha_2^{k+1}$和$\alpha_1^{k+1}$的關系求出$\alpha_1^{k+1}$
5)按照4.3節的方法計算$b^{k+1}$和$E_i$
6)在精度e范圍內檢查是否滿足如下的終止條件:$$\sum\limits_{i=1}^{m}\alpha_iy_i = 0 $$ $$0 \leq \alpha_i \leq C, i =1,2...m$$ $$\alpha_{i}^{k+1} = 0 \Rightarrow y_ig(x_i)?\geq?1 $$ $$ 0 <\alpha_{i}^{k+1} < C ?\Rightarrow y_ig(x_i)??=?1 $$ $$\alpha_{i}^{k+1}=?C \Rightarrow y_ig(x_i)??\leq 1$$
7)如果滿足則結束,返回$\alpha^{k+1}$,否則轉到步驟2)。
?
svm支持向量機原理。 SMO算法終于寫完了,這塊在以前學的時候是非常痛苦的,不過弄明白就豁然開朗了。希望大家也是一樣。寫完這一篇, SVM系列就只剩下支持向量回歸了,勝利在望!
(歡迎轉載,轉載請注明出處。歡迎溝通交流: liujianping-ok@163.com)?